神经网络和反向传播算法 Artificial Neural Network & BP

用通俗易懂的语言谈谈机器学习中的神经网络和 BP 算法。

Neural

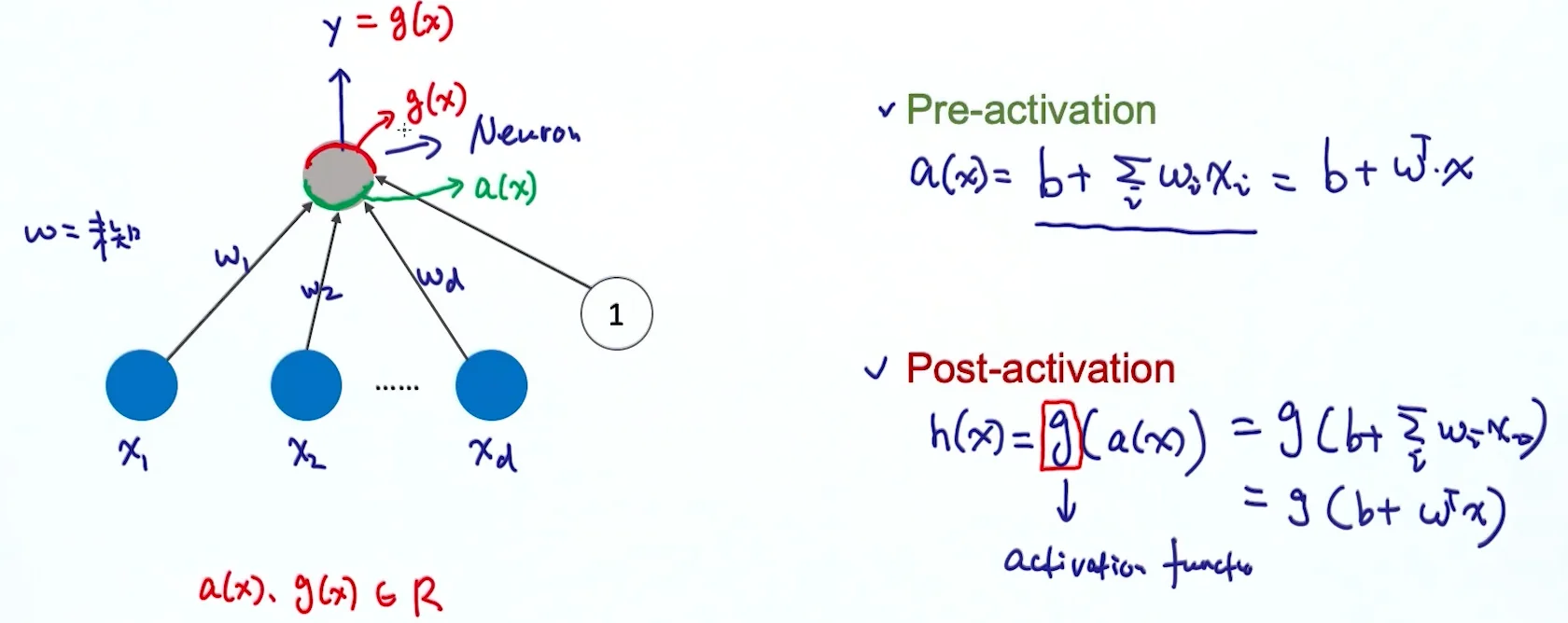
神经元的输入是一些信号，通过一系列的转换，输出另一种信号，再传给下一层神经元。

一个神经元的内部，对信号的处理分为两部分：

Pre-activation: \(a(x) = b + \sum_i w_ix_i = b+w^T \cdot x\)
Post-activation: \(h(x) = g(a(x)) = g(b+w^Tx)\)
- \(g(x)\) is an activation function

Activation Function

下面来说一说不同种类的激活函数。

Linear Activation Function

\[ g(a) = a \]

线性激活函数对输入没有任何处理，输出即输入。

它的特点是：

No bound（无上下限。）
Not interesting（没多大意义。）

通常出现在神经网络的最后一层。尤其是回归问题中。

线性激活函数的无意义体现在：假设输入 \(x\)，下面是每层神经元的输出：

\(w^{(1)}x\)
\(w^{(2)}(w^{(1)}x)\)
\(w^{(3)}[w^{(2)}(w^{(1)}x)]\)
...

每一层，对变量 \(x\) 进行的都是线性转换。等价地，最终对 \(x\) 进行了一层的线性转换（\(w'x\)）。所以这么多层的效果和一层的效果一样，很傻。

所以，通常神经网络的每一层，一定是产生了非线性转换，这样才有意义。

Sigmoid Activation Function

\[ g(a) = \frac{1}{1+e^{-a}} \]

Sigmoid 函数经常被使用。

它的特点：

Squash input（输入值都映射到了 \((0,1)\)）
Bounded（值域：\((0,1)\)）
Strictly increasing（严格单调递增函数）

Sigmoid 激活函数在神经网络中与逻辑回归模型的联系

如果使用 sigmoid function，可以发现输出是： \[ g(w^Tx) = \frac{1}{1+e^{-w^Tx}} \] 即逻辑回归（Logistic Regression）模型。

从这个角度，我们可以理解「逻辑回归是神经网络的一个特例」。

Logistic regression is a special case of neural network.

Hyperbolic Tangent (\(\tanh\)) Function

\[ g(a) = \tanh(a) = \frac{\exp(a) - \exp(-a)}{\exp(a) + \exp(-a)} = \frac{\exp(2a)-1}{\exp(2a)+1} \]

它的特点和 sigmoid 函数类似：

Squash input（输入值都映射到了 \((-1,1)\)）
Bounded（值域：\((-1,1)\)）
Strictly increasing（严格单调递增函数）

Rectifier Linear Activation Function (ReLU)

ReLu: Rectified Linear Unit.

\[ g(a) = \operatorname{ReLU}(a) = \max(0,a) \]

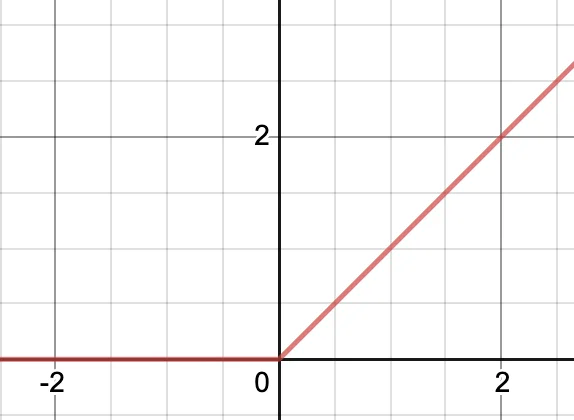
Boundary by \(0\)（部分有界限）
Not upper bounded（无上限）
Strictly increasing（\(x > 0\) 时，严格单调递增函数）
Sparse Activation（与 Lasso 算法类似，当输入小于某个值时，强制设置为 \(0\)，所以有稀疏的特点）

Layout

Single Hidden Layer Neural Network

我们先来看拥有「一层隐含层（Hidden Layer）」的神经网络。

关于层数的计算：注意，在文献中，关于计算这种网络的层数，有一些令人困惑的地方。图中的网络可能被描述成一个三层网络（计算单元的层数，把输入当成单元），或者有时作为一个单一隐含层网络（计算隐含单元层的数量）。我们推荐的计算方法是把图中的网络称为两层网络，因为它是可调节权值的层数，这对于确定网络性质很重要。

神经网络与感知器的区别：神经网络模型由两个处理阶段组成，每个阶段都类似于感知器模型，因此神经网络也被称为多层感知器（multilayer perceptron），或者 MLP。然而，与感知器模型相比，一个重要的区别是神经网络在隐含单元中使用连续的 sigmoid 非线性函数，而感知器使用阶梯函数这一非线性函数。这意味着神经网络函数关于神经网络参数是可微的，这个性质在神经网络的训练过程中起着重要的作用。

图中：

输入层 \(x\)
隐含层
- \(a(x)_i\) 是第 \(i\) 个神经元的 pre-activation，\(a(x) = (a(x)_1, a(x)_2, ... ,a(x)_{d'})\)
- \(h(x)_i\) 是第 \(i\) 个神经元的 post-activation，\(h(x) = (h(x)_1, h(x)_2, ... ,h(x)_{d'})\)
输出层
- 注意它也有 pre-activation & post-activation 两个阶段

我们看看每一层发生了什么。

对于第 \(i\) 个神经元：

隐含层中： \[ a(x)_i = \sum_j w_{ij}^{(1)} x_j + b_i^{(1)} \]

\[ h(x)_i = g(a(x)_i) = g(\sum_j w_{ij}^{(1)} x_j + b_i^{(1)}) \]

其中，\(g\) 是这一层的激活函数。

输出层中：（此处直接给出两个阶段的合并式） \[ \begin{align*}f(x) &= o(\sum _{j=1} ^{d'} w_j^{(2)} h(x)_j + b^{(2)}) \\&= o(w^{(2)} h(x) + b^{(2)})\end{align*} \] 其中，\(o\) 是这一层的激活函数。这里的激活函数具体是什么，取决于问题本身。比如，分类问题中，可以是 softmax 函数；回归问题中，可以是线性激活函数。

Example: Multiple Outputs in Classification Problem - Softmax Function & Cross Entropy

神经网络的输出层一般单独考虑并计算。具体地，考虑多分类问题中，神经网络有多个输出向量。

我们重点关注输出层。这里，\(a^{(2)}(x)\) 是输出层的 pre-activation。这里是一个三维向量 \(a^{(2)}(x) = \left(a^{(2)}(x)_1,a^{(2)}(x)_2,a^{(2)}(x)_3\right)\)。也就是说，是个三分类问题。\(h^{(2)}(x)\) 是 post-activation： \[ h^{(2)}(x) = o(a^{(2)}(x)) \] 这种情况下，我们常采用的激活函数 \(o\) 是 softmax。然后，\(h^{(2)}(x)_i\) 便可以代表输入属于分类 \(i\) 的概率了。

softmax 的定义是： \[ \sigma(\mathbf{z})_{i}=\frac{e^{z_{i}}}{\sum_{j=1}^{K} e^{z_{j}}} \text { for } i=1, \ldots, K \text { and } \mathbf{z}=\left(z_{1}, \ldots, z_{K}\right) \in \mathbb{R}^{K} \] 在这个例子中： \[ \begin{align*}h^{(2)}(x)_1 &= \frac{\exp(a^{(2)}(x)_1)}{\exp(a^{(2)}(x)_1) + \exp(a^{(2)}(x)_2) + \exp(a^{(2)}(x)_3)} \\h^{(2)}(x)_2 &= \frac{\exp(a^{(2)}(x)_2)}{\exp(a^{(2)}(x)_1) + \exp(a^{(2)}(x)_2) + \exp(a^{(2)}(x)_3)} \\h^{(2)}(x)_3 &= \frac{\exp(a^{(2)}(x)_3)}{\exp(a^{(2)}(x)_1) + \exp(a^{(2)}(x)_2) + \exp(a^{(2)}(x)_3)} \\\end{align*} \] 它们的和是 \(1\)，所以可以看作概率分布。

假设模型的输出概率 \(h(x) = (0.3, 0.6, 0.1)\)，真实的分类情况是 \(y = (0,1,0)\)。为了计算二者的差异（loss），以便有个指标（损失函数）来使它最小，我们采用交叉熵（Cross Entropy）来计算损失函数。 \[ l(h(x), y) = -(0\log0.3+1\log0.6+0\log0.1) = -\log0.6 \] 更一般地： \[ l\left(f\left(x\right), y\right)=-\sum_{c} I(y=c)-\log f(x)_c = -\log f(x)_y \]

其中， \(I\) 是指示器函数（Indicator Function），\(I(\exp) = 1 \text{ if exp is true}\).

可以看出，交叉熵的结果仅跟目标数值是 \(1\) 的分类有关。

Multi-Layer Neural Network

现在来看看多层神经网络。假如有 \(L\) 层隐含层。

对于第 \(k\) 层：

Pre-activation： \[ a^{(k)}(x) = w^{(k)}h^{(k-1)}(x) + b^{(k)} \] Post-activation： \[ h^{(k)}(x) = g(a^{(k)}(x)) \] 对于输出层： \[ h^{(L+1)}(x) = o(a^{(L+1)}(x)) = o(w^{(L+1)} h^{L}(x)+b^{(L)}) \]

Neural Network Training

Universal Approximation Theorem

在训练神经网络钱，我们来了解一下万能近似定理（Universal Approximation Theorem，一译「通用近似定理」、「通用逼近定理」等）。

A single hidden layer neural network with linear activation output, can approximate any continuous function arbitrary well, given enough hidden units. (Hornik, 1991)

一个带有线性输出的两层网络（即拥有一层隐含层的网络）可以在任意精度下近似任何输入变量较少的连续函数,只要隐含单元的数量足够多。

这个结果对于一大类隐含单元激活函数都成立,但是不包括多项式函数。

神经网络本质上是输入 \(x\) 到输出 \(y\) 的映射 \(f(x)\)。万能近似定理指的是对于任意复杂度的 \(f(x)\)，神经网络只需要一层隐含层就近似可以模拟出这个映射函数。

换句话说，一层隐含层的神经网络的表达能力就很强了！

However, this is a good result, but it doesn't mean there is a learning algorithm that can find the necessary parameter values.

但是，这虽然是一个很好的结果，但这并不意味着有一种学习算法可以找到必要的参数值。

很可惜，这只是一个理想情况。前提是要学习出理想的参数。但找到一个完美的学习方法来学习完美的参数，很难。

Loss Function

一个常用的思路是求出损失函数之后，进行梯度下降法来求最优参数 \(\theta\)。最优化问题是： \[ \underset{\theta}{\operatorname{argmin}} \frac{1}{T} \sum_t l\left(f(x^{(t)};\theta), y^{t}\right) + \lambda \Omega(\theta) \]

\(l\): 损失函数
\(\theta\): 参数集合 \(\{(w^{(i)}, b^{(i)})^{L=1}_{i=1}\}\)
\(f\): 模型激活函数
\(y\): 目标实际值
\(\lambda \Omega(\theta)\): 正则项

在梯度下降法（SGD）中：

初始化 \(\theta = \{w^{(1)}, b^{(1)}, ...,w^{(L+1)}, b^{(L+1)}\}\)
for N iterations:
1. for each training set \((x^{(t)}, y^{(t)})\):
  1. \(\Delta = -\nabla_{\theta} l\left(f\left(x^{(t)} ; \theta\right), y^{(t)}\right)-\lambda \nabla_{\theta} \Omega(\theta)\)
  2. \(\theta = \theta + \alpha \Delta\)

这里的 \(l\) 具体是什么，将取决于问题的类型。比如上面例子的多分类问题中，我们在最后一层使用 softmax 激活函数，然后损失函数用的是交叉熵（Cross Entropy）。

Backpropagation

误差反向传播算法（Backpropagation）的目的是寻找一种计算神经网络的误差/损失函数的梯度的高效方法。

整个梯度的计算将针对五个模块：

输出层的 post-activation \(\frac{\partial l}{\partial f(x)}\)
输出层的 pre-activation \(\frac{\partial l}{\partial a^{(L+1)}(x)}\)
隐含层的 post-activation \(\frac{\partial l}{\partial h^{(k)}(x)}\), \(K = 1,...,L\)
隐含层的 pre-activation \(\frac{\partial l}{\partial a^{(k)}(x)}\), \(K = 1,...,L\)
参数 \(\frac{\partial l}{\partial w^{(k)}}\), \(\frac{\partial l}{\partial b^{(k)}}\), \(K = 1,...,L\)

假设输出层的激活函数是 softmax 函数，损失函数 \(l\) 是交叉熵函数。我们依次看每个步骤。

输出层的 Post-Activation

对于单个神经元 \(c\)： \[ \begin{align*}\frac{\partial l}{\partial f(x)_c} &= \frac{\partial - \log f(x)_y}{\partial f(x)_c} \\&= \frac{-1}{f(x)_{y}} \cdot \frac{\partial f(x)_{y}}{\partial f(x)_{c}} \\&= -\frac{I(y=c)}{f(x)_{y}}\end{align*} \] 那么，对于全部神经元： \[ \begin{align*}\frac{\partial l}{\partial f(x)} &= \frac{\partial - \log f(x)_y}{\partial f(x)} \\&= -\frac{I(y=c)}{f(x)_{y}} \\&= -\frac{1}{f(x)_{y}} \cdot \left(\begin{array}{c}{I(y=1)} \\ {I(y=2)} \\ {\vdots} \\ {I(y=k)}\end{array}\right) \\&= -\frac{e(y)}{f(x)_{y}}\end{align*} \] 其中，\(e(y) = (0,1,0,...)\) 的形式，是 one-hot encoding。

输出层的 Pre-Activation

对于单个神经元 \(c\)： \[ \begin{align*}\frac{\partial l}{\partial a^{(L+1)}(x)_c} &= \frac{\partial - \log f(x)_y}{\partial a^{(L+1)}(x)_c} \\&= -\frac{1}{f(x)_{y}} \cdot \frac{\partial f(x)_{y}}{\partial a^{(L+1)}(x)_c} \\&= -\frac{1}{f(x)_{y}} \cdot \frac{\partial \frac{\exp \left(a^{(L+1)}(x)_{y}\right)}{\sum_{c'} \exp \left(a^{(L+1)}(x)_{c^{\prime}}\right)}}{\partial a^{(L+1)}(x)_c} \\&= -\frac{1}{f(x)_{y}} \cdot \left(\frac{\frac{\partial}{\partial a^{(L+1)}(x)_c} \cdot \exp \left(a^{(L+1)}(x)_{y}\right)}{\sum_{c'} \exp\left(a^{(L+1)}(x)_{c'}\right)}-\frac{\exp \left(a^{(L+1)}(x)_y \right) \frac{\partial \sum_{c'}\exp\left( a^{(L+1)}(x)_{c'} \right)} {\partial a^{(L+1)}(x)_{c}}}{\left( \sum_{c^{\prime}} \exp \left(a^{(L+1)}(x)_{c'}\right)\right)^{2}}\right) \\&= -\frac{1}{f(x)_{y}} \cdot \left(\frac{\exp \left(a^{(L+1)}(x)_{y}\right) I(y=c)}{\sum_{c'} \exp\left(a^{(L+1)}(x)_{c'}\right)}-\frac{\exp \left(a^{(L+1)}(x)_y \right) \exp \left(a^{(L+1)}(x)_c \right)}{ \sum_{c^{\prime}} \exp \left(a^{(L+1)}(x)_{c'}\right) \cdot \sum_{c^{\prime}} \exp \left(a^{(L+1)}(x)_{c'}\right) }\right) \\&= -\frac{1}{f(x)_{y}} \cdot \left( \operatorname{softmax} \left(a^{(L+1)}(x)\right)_{y} \cdot I(y=c) - \operatorname{softmax} \left(a^{(L+1)}(x)\right)_{y} \cdot \operatorname{softmax} \left(a^{(L+1)}(x)\right)_{c} \right) \\&= -\frac{1}{f(x)_{y}} \left( f(x)_y \cdot I(y=c) - f(x)_y \cdot f(x)_c \right) \\&= -\left(I(y=c) - f(x)_c\right) \\&= f(x)_c - I(y=c)\end{align*} \] 那么，对于全部神经元： \[ \begin{align*}\frac{\partial l}{\partial a^{(L+1)}(x)}&= f(x) - e(y)\end{align*} \]

隐含层的 Post-Activation

预备知识：链式求导 \[ \frac{\partial A}{\partial B}=\sum_{i=1}^{n} \frac{\partial A}{\partial C_{i}} \cdot \frac{\partial C_{i}}{\partial B} \\\frac{\partial A}{\partial B}= \frac{\partial A}{\partial C} \cdot \frac{\partial C}{\partial B} \]

对于 \(k\) 层单个神经元 \(c\)： \[ \begin{align*}\frac{\partial l}{\partial h^{(k)}(x)_c} &= \sum_i \frac{\partial l}{\partial a^{(k+1)}(x)_i} \cdot \frac{\partial a^{(k+1)}(x)_i}{\partial h^{(k)}(x)_c} \\&= \sum_i \frac{\partial l}{\partial a^{(k+1)}(x)_i} \cdot \frac{\partial \sum_j w_{ij}^{(k+1)} h^{(k)}(x)_j}{\partial h^{(k)}(x)_c} \\&= \sum_i \frac{\partial l}{\partial a^{(k+1)}(x)_i} \cdot w_{ij}^{(k+1)} \\&= \frac{\partial l}{\partial a^{(k+1)}(x)} \cdot w_{\cdot j}^{(k+1)} \\&= (w_{\cdot j}^{(k+1)})^T \cdot \frac{\partial \log f(x)_y}{\partial a^{(k+1)}(x)}\end{align*} \] 那么，对于 \(k\) 层全部神经元： \[ \begin{align*}\frac{\partial l}{\partial h^{(k)}(x)}&= w^{(k+1)} \cdot \frac{\partial \log f(x)_y}{\partial a^{(k+1)}(x)}\end{align*} \]

隐含层的 Pre-Activation

对于 \(k\) 层单个神经元 \(c\)： \[ \begin{align*}\frac{\partial l}{\partial a^{(k)}(x)_c} &= \frac{\partial l}{\partial h^{(k)}(x)_c} \cdot \frac{\partial h^{(k)}(x)_c}{\partial a^{(k)}(x)_c} \\ &= \frac{\partial l}{\partial h^{(k)}(x)_c} \cdot \frac{\partial g(a^{(k)}(x)_c)}{\partial a^{(k)}(x)_c} \\ &= \frac{\partial l}{\partial h^{(k)}(x)_c} \cdot g'(a^{(k)}(x)_c) \end{align*} \] 那么，对于 \(k\) 层全部神经元： \[ \begin{align*}\frac{\partial l}{\partial a^{(k)}(x)}&= \frac{\partial l}{\partial h^{(k)}(x)} \circ g'(a^{(k)}(x)) \end{align*} \] 其中，\(\circ\) 表示阿达玛乘积（Hadamard Product），又叫逐项积（Element-Wise Product）。其输入为两个相同形状的矩阵，输出是具有同样形状的、各个位置的元素等于两个输入矩阵相同位置元素的乘积的矩阵。

参数

对于 \(k\) 层第 \(i\) 个神经元的第 \(j\) 个参数 \(w\)： \[ \begin{align*}\frac{\partial l}{\partial w_{ij}^{(k)}} &= \frac{\partial l}{\partial a^{(k)}(x)_i} \cdot \frac{ {\partial a^{(k)}(x)_i}}{\partial w_{ij}^{(k)} } \\&= \frac{\partial l}{\partial a^{(k)}(x)_i} \cdot \frac{ {\partial \sum_j w_{ij}^{(k)} h^{(k-1)}(x)_j}}{\partial w_{ij}^{(k)} } \\&= \frac{\partial l}{\partial a^{(k)}(x)_i} \cdot h^{(k-1)}(x)_j \\&= \frac{\partial - \log f(x)_y}{\partial a^{(k)}(x)_i} \cdot h^{(k-1)}(x)_j \\\end{align*} \] 那么，对于 \(k\) 层全部参数 \(w\)： \[ \begin{align*}\frac{\partial l}{\partial w^{(k)}} &= \frac{\partial - \log f(x)_y}{\partial a^{(k)}(x)_i} \cdot (h^{(k-1)}(x))^T \\\end{align*} \] 对于 \(k\) 层第 \(i\) 个神经元的参数 \(b\)： \[ \begin{align*}\frac{\partial l}{\partial b_{i}^{(k)}} &= \frac{\partial l}{\partial a^{(k)}(x)_i} \cdot \frac{ {\partial a^{(k)}(x)_i}}{\partial b_{i}^{(k)} } \\&= \frac{\partial l}{\partial a^{(k)}(x)_i} \\&= \frac{\partial - \log f(x)_y}{\partial a^{(k)}(x)_i}\end{align*} \] 那么，对于 \(k\) 层全部参数 \(w\)： \[ \begin{align*}\frac{\partial l}{\partial b^{(k)}}&= \frac{\partial - \log f(x)_y}{\partial a^{(k)}(x)}\end{align*} \]

BP Procedures

下面，对上面的五个部分进行总结。

For training data \((x,y)\)：

Compute output gradient
1. \(\nabla a^{(L+1)}(x)-\log f(x)_y= \color{red}{f(x)}-e(y)\)
For \(k = L+1\) to \(1\)
1. Compute gradient of parameters
  1. \(\nabla w^{(k)}-\log f(x)_{y}=\left(\nabla a^{(k)}(x) -\log f(x)_{y}\right) \cdot \left(\color{red}{h^{(k+1)}(x)}\right)^T\)
  2. \(\nabla b^{(k)}-\log f(x)_{y}=\nabla a^{(k)}(x) -\log f(x)_{y}\)
2. Compute gradient of hidden layers
  1. \(\nabla h^{(k-1)}-\log f(x)_{y}=\left(\nabla a^{(k)}(x) -\log f(x)_{y}\right) \cdot \left(w^{(k)}\right)^T\)
  2. \(\nabla a^{(k-1)}-\log f(x)_{y}=\left( \nabla h^{(k-1)}-\log f(x)_{y} \right) \circ g'(\color{red}{a^{(k-1)}(x)})\)

注意其中的红色项，是提前在正向传播算法中获得的。

所以整个 BP 算法分为三个阶段：

Forward propagation
1. Compute \(f(x), \{a^{(k)}(x), h^{(k)}(x) \}\)
Backward propagation
1. Compute gradient of parameters and hidden layers
Update parameters

Gradient Checking

怎么确保 BP 算法的计算过程（尤其在实现中）完全正确呢？

梯度的定义是这样的： \[ f'(x)=\frac{\partial f(x)}{\partial x}=\frac{f(x+\epsilon)-f(x-\epsilon)}{2 \epsilon} \] \(\epsilon\) 是个很小的数字（比如 \(10^{-8}\)）。当它无限小时，我们可以认为梯度即公式计算出的导数。

所以在程序中，我们可以用这种代码： \[ \left|\frac{f(x+z)-f(x-\varepsilon)}{2 \varepsilon}-\frac{\partial f(x)}{\partial x}\right|<10^{-6} \] 探测误差。如果超出阈值，就要注意一下了。

Optimization for Deep Learning

深度学习是个很强的非凸函数（Highly Non-Convex Function）。很难找到全局最优解。哪怕找到很好的局部最优解也很难。训练起来也很难。

Plateau

其中一个难点就是损失函数的形状上。我们经常会在地形平缓的「伪最优」区域提前中止梯度下降。为了解决这个问题，momentum 可以帮助我们在这个地形有一个更大的动量去探索。

Learning Rate: SGD with Converge

梯度下降法什么时候可以保证一定收敛呢？理论上，需要满足下面两个条件：

\(\sum_{t=1}^{\infty} \eta_t = \infty\)
\(\sum_{t=1}^{\infty} \eta_t^2 \lt \infty\)

至于原因，在此就不深入探究了……

举个例子，\(\eta_t = \frac{1}{2^t}\) 很显然不满足第一个条件，就不是个好的步长。

一些比较好的例子有：

\(\eta_t = \frac{\alpha}{1+\delta_t}\)，\(\delta\) 是 decrease constant。随着时间推移，会越来越大，使得步长越来越小
\(\eta_t = \frac{\alpha}{t^{\delta}}\)，\(\delta \in (0.5,1)\)

但是建议，一开始解决问题时，先设置为固定步长，不要让程序掺入过多不确定的参数，以便 debug……程序跑通后，再去调整步长。

Early Stopping (with Look Ahead)

为了解决过拟合问题，提前结束下降可以模型过度被训练，不失为一个好办法。

一图胜千言：

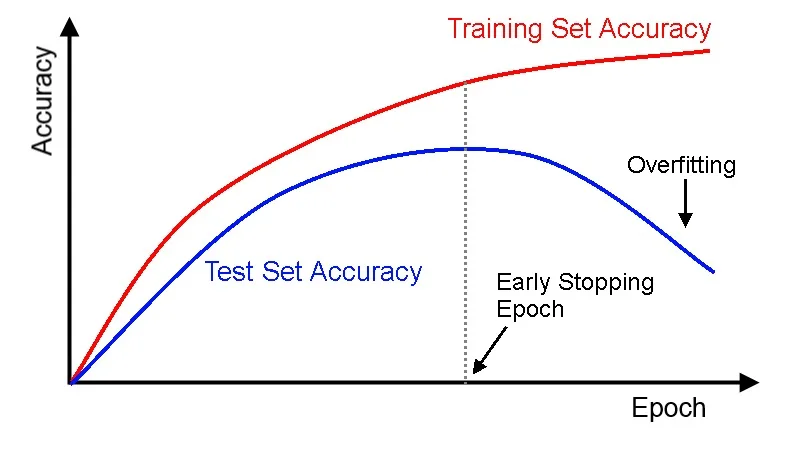
在虚线左边是欠拟合（under-fitting），右边是过拟合（over-fitting），而中间是最佳的提前结束点。

但是需要注意的是，需要多看一些迭代，不能一看趋势不好就提前停止，说不定后面还有更好的选择。

另外一点，这两条线之间的 gap 在模型越复杂时，会变得越大。而我们是希望这个 gap 越小越好。