用通俗易懂的语言谈谈机器学习中的支持向量机。
线性支持向量机(Linear SVM)
决策边界
回顾一下决策边界的知识。
决策边界怎么求呢?求法是基于这样一个性质:落在决策边界上的点,对于两边的概率是相等的,即 \(P(y=0|x,w) = P(y=1|x,w)\)。
基于: \[ \begin{align} P(y = 1 |x,w) &= \frac{1}{1+e^{-(w^T x + b)}} \\ \\ P(y = 0 |x,w) &= 1 - P(y = 1 |x,w) \\ & = \frac{e^{-(w^T x + b)}}{1+e^{-(w^T x + b)}} \end{align} \]
两个式子可以合并成:\(P(y|x,w) = P(y=1|x,w)^y [1-P(y=1|x,w)]^{1-y}\)。
我们把上面两个式子代入到 \(P(y=0|x,w) = P(y=1|x,w)\): \[ \begin{align} \frac{e^{-(w^T x + b)}}{1+e^{-(w^T x + b)}} &= \frac{1}{1+e^{-(w^T x + b)}} \\ e^{-(w^T x + b)} &= 1 \\ \ln e^{-(w^T x + b)} &= \ln 1 \\ -(w^T x+b) &= 0 \\ w^T x+b &= 0 \end{align} \] 那么最后的 \(w^T x+b = 0\) 就是逻辑回归的决策边界。它是线性的。
有了决策边界,我们就可以决策一个样本是属于 \(y = 1\) 还是 \(y = -1\) 了。比如说: \[ \left\{\begin{array}{l}{w^Tx_i +b \ge 0 \to y_i = 1 \\ w^Tx_i +b \lt 0 \to y_i = -1}\end{array}\right. \] 上面两个情况可以合并成: \[ (w^Tx_i +b) \cdot y_i \ge 0 \] 这个不等式使用频率挺高。
最大间隔分类
考虑这个案例:下面三个线性分类器,哪个最佳?

答案是第二条。为什么不是另外两条呢?因为某些点离他们过近,假如我加入一些噪音干扰(Perturbations),这些点可能就移动到了线的另一端,这些线就不准确了,就被称作鲁棒性(Robustness)弱。
如果我们作两条平行切线,可以发现,第二条线(也是平行的)在「安全区域内」离两线边距(Margin)最大。

所以我们可以通过这种方式来寻找一个最优的决策边界。这种方式也叫做最大间隔分类(Max-Margin Method)。
具体做法是,先对三条平行线进行定义,并且不难看出,它们的垂线是 \(w\):
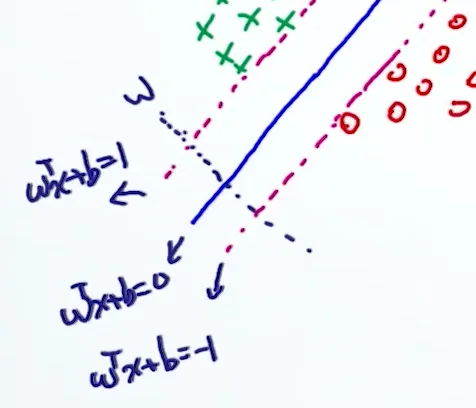
为了证明垂线是 \(w\),我们在 \(wx+b=0\) 上取两点 \(w_1\), \(w_2\),有 \(wx_1+b =0\), \(wx_2+b =0\),相减得 \(w(x_1-x_2) = 0\),即 \(w \perp\left(x_{1}-x_{2}\right)\)。
我们再在上面直线上取 \(x_+\),在下面直线上取 \(x_-\),使得 \(x_+ = x_- + \lambda w\)。根据定义,又有 \(w^Tx_+ +b=1\),\(w^Tx_{-}+b=-1\)。
把 \(x_+ = x_- + \lambda w\) 代入 \(w^Tx_+ +b=1\): \[ w^T(x_- + \lambda w) +b=1 \\w^Tx_- + \lambda w^Tw +wb=1 \\\lambda w^Tw =2 \\\lambda = \frac{2}{w^Tw} \\ \] 把 \(x_+ = x_- + \lambda w\) 代入 margin 的表达式中: \[ \begin{align*}\text{margin} &= |x_+ - x_-| \\&= |\lambda w| \\&= \lambda |w| \\&= \frac{2}{w^Tw} \cdot \| w \| \\&= \frac{2}{ \| w \|} \end{align*} \] 我们的目标就是让 margin 最大,也就是让 \(\frac {2} { \| w \| }\) 最大。
Hard Constraint
也就是说,我们要让 $ $ 最大,使得: \[ \left\{\begin{array}{l}{w^{T} x_{i}+b \ge 1} & {\text { if } y_{i}=1} \\ {w^T x_{i}+b\le-1} & {\text { if } y_{i}=-1}\end{array}\right. \] 如果转化成最小化问题就是:我们要让 \(\|w\|\) 最小,或者可以说让 \(\|w\|^2\) 最小(方便后续计算),使得: \[ (w^T x_i+b)y_i \ge 1 \]
这种模型我们管它叫限制性优化(Constrained Optimization)问题。
但这种限制条件其实不是很好。比如下面这个案例:

可以看出,满足这个严格条件的线,会导致过拟合。
Soft Constraint
那我们把条件松弛一些不就可以了嘛?
也就是,让 \(\|w\|^2 + \lambda \sum^n_{i=1} \epsilon_i\) 最小,使得: \[ (w^T x_i+b)y_i \ge 1 - \epsilon_i \] 其中,\(\epsilon_i \ge 0\),叫做松弛变量(Slack Variable),代表了一个允许犯错的程度(Degree of Mistake)。并且我们希望这个错误不要太大,所以在目标函数里加上了 \(\lambda \sum^n_{i=1} \epsilon_i\),\(\lambda\) 就是目标函数的两项的平衡关系,越大越不让犯错。
之所以 \(\epsilon_i \ge 0\),是因为如果 \(\epsilon_i \le 0\),这个错误容忍反而南辕北辙。
铰接损失(Hinge Loss)
再进一步思考,我们能不能把上面的这个限制条件转化到目标函数 \(\|w\|^2 + \lambda \sum^n_{i=1} \epsilon_i\) 里面呢?
很简单,由 \((w^T x_i+b)y_i \ge 1 - \epsilon_i\) 这个条件,可以得到: \[ \epsilon_i \ge 1 - (w^T x_i+b)y_i \] 也就是说,\(\epsilon_i\) 的最小值就是 \(1 - (w^T x_i+b)y_i\)。同时注意 \(\epsilon_i \ge 0\)。所以,目标函数就是: \[ \|w\|^2 + \lambda \sum^n_{i=1} \max(0,1 - (w^T x_i+b)y_i) \] 上面的 \(\max(0,1 - (w^T x_i+b)y_i)\) 叫做铰接损失(Hinge Loss)。
在机器学习中,铰接损失是一个用于训练分类器的损失函数。铰链损失常被用于“最大间隔分类”,尤其适用于支持向量机 (SVMs)。对于一个预期输出 \(t = ±1\),分类结果 \(y\) 的铰接损失定义为 \({\displaystyle \ell (y)=\max(0,1-t\cdot y)}\)。
目标求最优
随机梯度下降法(Stochastic Gradient Descent)
- init \(w_0\), \(b_0\)
- for \(i = 1...n\)
- if \(1-y_i (w^T x_i + b) \lt 0\)
- \(w^* = w - \eta_t \cdot 2w\)
- else
- \(w^* = w - \eta_t (2w+\lambda \frac{\part (1-y_i (w^T x_i + b))}{\part w})\)
- \(b^* = b - \eta_t(\lambda\frac{\part (1-y_i (w^T x_i + b))}{\part b})\)
- if \(1-y_i (w^T x_i + b) \lt 0\)
Linear SVM 的缺点
下面这些非线性的情况,Linear SVM 就无法适用了。

解决办法有:
- 利用非线性模型代替(比如神经网络)
- 把数据映射到高维空间,在高维空间学习线性模型
我们主要来看第二种方法。
非线性模型的处理
数据映射到高维空间(High Dimensional Space)
我们的思路是:假如说,我们有一个向量 \(x = \left(\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {\vdots} \\ {x_{D}}\end{array}\right)\)。现在我们需要一个「非线形变化器 \(\phi\)」,来把这个向量映射成高维空间的向量 $(x) = u = (\begin{array}{c}{u_{1}} \ {u_{2}} \ {} \ {u_{D'}}\end{array}) $,此处的 \(D' \gg D\)。再对这些向量进行线性回归分析 \(f(\phi(x)) = y\)。
这个思路不错,但是有一个问题。假如原先的 \(x\) 是 10 维,现在经过映射可以变成 1000 维。这中间的映射过程需要 \(10^3\) 的时间复杂度。而之后构建模型时,复杂度也会由 \(O(D)\) 变成 \(O(D')\),即 \(10^4\)。
这个耗时的问题如何解决?
Lagrangian: From Constrained To Unconstrained
我们先来学习一个叫拉格朗日乘子的知识。
之前提到的,类似下面这种形式的: \[ \begin{array}{cl}{\min } & {f(\mathrm{x})} \\ {\mathrm{subject} \text { to }} & {g_{i}(\mathrm{x})=c_{i} \quad \text { for } i=1, \ldots, n \quad \text { Equality constraints }} \\ {} & {h_{j}(\mathrm{x}) \geqq d_{j} \text { for } j=1, \ldots, m \quad \text { Inequality constraints }}\end{array} \] 都叫 Constrained Optimization。
现在我们希望可以有一个办法,能把 Constrained Optimization 变成 Unconstrained Optimization。
这个办法就是拉格朗日乘子法(Lagrangian)。
单相等限制的情况处理
首先来看相等情况下的处理方式。
所有类似这种形式的 Constrained Optimization: \[ \begin{array}{cl}{\min } & {f(x)} \\ {\mathrm{subject} \text { to }} & {g(x) = 0}\end{array} \] 都可以转化成下面的 Unconstrained Optimization: \[ \min f(x) + \lambda g(x) \]
举个例子,假如我们要求: \[ \begin{array}{cl}{\min } & {x_1^2 + x_2^2} \\ {\mathrm{subject} \text { to }} & {x_2-x_1 = -1}\end{array} \] 经过转换之后,变成了: \[ \min x_1^2 + x_2^2 + \lambda (x_1^2 + x_2^2+1) \] 设它为 \(L(x,\lambda)\),对每个参数分别求导,并令其等于 \(0\): \[ \left(\begin{array}{c}{\frac{\partial L}{\partial x_{1}}} \\ {\frac{\partial L}{\partial x_{2}}} \\ {\frac{\partial L}{\partial \lambda}}\end{array}\right)=\left(\begin{array}{c}{2 x_{1}-\lambda} \\ {2 x_{2}-\lambda} \\ {x_{2}-x_{1}+1}\end{array}\right)=\left(\begin{array}{l}{0} \\ {0} \\ {0}\end{array}\right) \] 然后求解方程,得: \[ \left(\begin{array}{l}{x_{1}} \\ {x_{2}}\end{array}\right)=\left(\begin{array}{c}{\frac{1}{2}} \\ {-\frac{1}{2}}\end{array}\right) \]
但是为什么呢?
我们还是基于这个例子,来看看它的几何含义:
当 \(x_1^2 + x_2^2\) 表示的圆形与 \(x_2-x_1 = -1\) 表示的直线相切,满足最小条件。此时,圆在点 \((\frac{1}{2}, -\frac{1}{2})\) 的切线与直线的斜率相等,即两条直线平行。
\(f(x)\) 与 \(g(x)\) 斜率相等,可以写成这种表达式: \[ \begin{align*} \nabla_{x} f(x) = \pm \lambda \nabla_{x} g(x) \\ \nabla_{x} f(x) \mp \lambda \nabla_{x} g(x) = 0 \\ \nabla_{x}(f(x) \mp \lambda g(x)) = 0 \end{align*} \] 那也就是我们的变化式 \(\min f(x) + \lambda g(x)\) 的导数等于 \(0\)。即: \[ \begin{array}{c}{\frac{\partial(f(x)+\lambda g(x))}{\partial x}=0} \\ {\frac{\partial(f(x)+\lambda g(x))}{\partial \lambda}=g(x)=0}\end{array} \]
\(g(x)=0\) 其实就是原始条件。
多相等限制的情况处理
接下来泛化一下场景,如果有多个相等条件怎么办呢?比如: \[ \begin{array}{cl}{\min } & {f(x)} \\ {\mathrm{subject} \text { to }} & {g_i(x) = 0} \quad \text{for } i=1,...,n \end{array} \] 这种情况下的转化,对每个条件分别应用上述转化,然后求和即可: \[ \min f(x) + \sum^n_{i=1}\lambda_i g_i(x) \]
不等限制的情况处理
接下来看看不等限制: \[ \begin{array}{cl}{\min } & {f(x)} \\ {\mathrm{subject} \text { to }} & {h(x) \le 0}\end{array} \] 它的转化是: \[ \begin{array}{cl}{\min } & {f(x) + \lambda h(x)} \\ {\mathrm{subject} \text { to }} & {h(x) \le 0 \\ \lambda h(x) = 0}\end{array} \] 我们分情况验证一下。
情况一:没有限制条件的最优解正好满足限制条件的解。也就是说,忽视条件,找出 \(f(x)\) 的最优解 \(x^*\),然后发现 \(x^*\) 刚好满足 \(h(x) \le 0\)。这种情况下,\(\lambda = 0\),\(h(x) \le 0\)。
情况二:没有限制条件的最优解不满足限制条件的解。这种情况下,为了满足条件,需要让 \(h(x)=0\),\(\lambda \gt 0\)。
将两种条件合并,得 \(\lambda h(x) = 0\)。
综合情况的处理: KKT
将以上几种情况综合: \[ \begin{array}{cl}{\min } & {f(\mathrm{x})} \\ {\mathrm{subject} \text { to }} & {g_{i}(\mathrm{x})=0 \quad \text { for } i=1, \ldots, n \quad \text { Equality constraints }} \\ {} & {h_{j}(\mathrm{x}) \le 0 \quad \text { for } j=1, \ldots, m \quad \text { Inequality constraints }}\end{array} \] 转化结果是: \[ \begin{array}{cl}{\min } & {f(x)+\sum_{i=1}^{n} \lambda_{i} g_{i}(x)+\sum_{j=1}^{m} \mu_{j} h_{j}(x)} \\ {\mathrm{subject} \text { to }} & {\lambda_i, \mu_j \gt 0 \quad \forall i,j \\ h_j(x) \le 0 \quad \forall j \\ \mu h_j(x) = 0 \quad \forall j}\end{array} \] 此处的三个条件,我们管它们叫做 KKT 条件(Karush-Kuhn-Tucker Conditions)。
Dual Derivation of SVM
Primal Form vs Dual Form
我们目前为止讨论的都是 Linear SVM 的原始形式(Primal Form)。它一般是以像这样的逻辑来分析问题的:\(min \ f(x) \ s.t. g_i(x) \le 0, ...\)。大多数情况下,我们建模都是按照这种形式。而有些比较难的场景,我们会考虑转化成等价的对偶形式(Dual Form)来更好地解决问题。
具体来说,有这么几个理由使用 Dual Form:
- Primal 问题有可能比较难解决
- 在 Dual 问题上有可能会发现一些有趣的 insight
但其实 Dual Form 拿到的最优解是 sub-optimal,与 Primal Form 拿到的 optimal 还是有差距的。但理想情况下,这二者之间的 gap 希望可以是 0。
问题解决思路
所以,遇到一个问题,我们可以先把它转化为一个数学问题,然后根据不同的问题类型,来选择相应的解题路径。如果走 Primal 路径,可以通过一些工具直接解决;但如果是 Dual 路径,还需要将问题进一步转化成 Dual 问题后,再尝试通过一些工具解决。通过 Dual 解决完后,还要判断一下,它和 Primal 解决出的结果之间的 gap。
Dual Form of SVM
我们现在来把 SVM 转化成 Dual Form。
回顾一下 SVM 的 Hard Constraint: \[ \begin{array}{cl}{\min } & {\frac{1}{2}\| w\|_2^2} \\ {\mathrm{subject} \text { to }} & {y_i(w^Tx_i+b) - 1 \ge 0 \quad \text{for } i =1,...,n}\end{array} \] 用拉格朗日乘子法转化: \[ \begin{array}{cl}{\min } & {\frac{1}{2}\| w\|_2^2 + \sum_{i=1}^n \lambda_i [1-y_i(w^Tx_i+b)]} \\ {\mathrm{subject} \text { to }} & {\lambda_i \ge 0 \quad \forall i \\ \lambda_i[1-y_i(w^Tx_i+b)] = 0 \quad \forall i \\ 1-y_i(w^Tx_i+b) \le 0 \quad \forall i}\end{array} \] 现在分别对参数进行求导: \[ \frac{\partial L}{\partial w} = w+\sum_{i=1}^{n} \lambda_{i}\left(-y_{i} x_{i}\right) = 0 \\\Downarrow \\w = \sum_{i=1}^{n} \lambda_{i} y_{i} x_{i} \]
\[ \frac{\partial L}{\partial b} = \sum_{i=1}^{n} \lambda_{i} y_{i}=0 \]
那么再分别看目标函数的两项: \[ \begin{align*} \frac{1}{2}\| w\|_2^2&=\frac{1}{2}w^Tw \\ &=\frac{1}{2}(\sum_{i=1}^{n} \lambda_{i} y_{i} x_{i})^T(\sum_{j=1}^{n} \lambda_{j} y_{j} x_{j}) \\ &=\frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n\lambda_i\lambda_jy_iy_jx_i^Tx_j \end{align*} \]
\[ \begin{align*} \sum_{i=1}^n \lambda_i [1-y_i(w^Tx_i+b)] &= \sum_{i=1}^{n} \lambda_{i}-\sum_{i=1}^{n} \lambda_{i} \cdot y_{i}\left(w^Tx_i+b\right) \\ &=\sum_{i=1}^{n} \lambda_{i}-\sum_{i=1}^{n} \lambda_{i} y_{i} w^Tx_{i}-\sum_{i=1}^{n} \lambda_{i} y_{i}b \\ &=\sum_{i=1}^{n} \lambda_{i}-\sum_{i=1}^{n} \lambda_{i} y_{i} w^Tx_{i} \\ &=\sum_{i=1}^{n} \lambda_{i}-\sum_{i=1}^{n} \lambda_{i} y_{i} (\sum_{j=1}^{n} \lambda_{j} y_{j} x_{j})^Tx_{i} \\ &=\sum_{i=1}^{n} \lambda_{i}-\sum_{i=1}^{n} \sum_{j=1}^{n} \lambda_{i} \lambda_{j} y_{i} y_{j} x_i^T x_j \end{align*} \]
那么,目标函数: \[ L = -\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \lambda_{i} \lambda_{j} y_{i} y_{j} x_{i}^{T}x_{j}+\sum_{i=1}^{n} \lambda_{i} \] 如此,我们便得到了 Dual Formation of SVM: \[ \begin{array}{cl}{\min } & {-\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \lambda_{i} \lambda_{j} y_{i} y_{j} x_{i}^{T}x_{j}+\sum_{i=1}^{n} \lambda_{i}} \\ {\mathrm{subject} \text { to }} & {\lambda_i \ge 0 \quad \forall i \\ \sum^n_{i=1}\lambda_i y_i = 0, \quad w=\sum_{i=1}^{n} \lambda_{i} y_{i} x_{i}\\\lambda_{i}\left[1-y_{i}\left(\omega^{\top} x_{i}+b\right)\right]=0}\end{array} \] 与 Primal 问题上的未知参数 \(w,b,\lambda\) 相比,Dual 形式只有一个未知参数 \(\lambda\)。\(w=\sum_{i=1}^{n} \lambda_{i} y_{i} x_{i}\),实际上可以看作「已知的」。
这个转化好在哪里呢?关键是 \(x_{i}^{T}x_{j}\) 这一项。有了这一项,我们才能做低维到高维的转换,也叫 Kernel Method / Kernel Trick。
Kernel Trick
从低维到高维
回顾一下我们的思路:假如说,我们有一个向量 \(x = \left(\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {\vdots} \\ {x_{D}}\end{array}\right)\)。现在我们需要一个「非线形变化器 \(\phi\)」,来把这个向量映射成高维空间的向量 $(x) = u = (\begin{array}{c}{u_{1}} \ {u_{2}} \ {} \ {u_{D'}}\end{array}) $,此处的 \(D' \gg D\)。再对这些向量进行线性回归分析 \(f(\phi(x)) = y\)。
假如说我们有两个向量 \(x = (x_1,x_2)\),\(z=(z_1,z_2)\),那么有: \[ x^Tz = x_1z_1 + x_2z_2 \] 假如,\(\phi(x) = (x_1^2, x_2^2, \sqrt{2}x_1x_2)\),\(\phi(z) = (z_1^2, z_2^2, \sqrt{2}z_1z_2)\),那么有: \[ \begin{align*} \phi(x^T)\phi(z) &= x_{1}^{2} z_{1}^{2}+x_{2}^{2} z_{2}^{2}+2 x_{1} x_{2} z_1z_{2} \\ &= (x_1z_1 + x_2z_2)^2 \\ &= (x^Tz)^2 \end{align*} \] 这里有一个很有趣的现象,两个向量在高维空间通过内积(Dot Product)出来的结果,和他们的(精心设计出来的)映射过程其实没有任何关系,而是仅仅依赖于原来空间的内积。
回头看看我们 Dual Form 下的的目标函数: \[ L = -\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \lambda_{i} \lambda_{j} y_{i} y_{j} x_{i}^{T}x_{j}+\sum_{i=1}^{n} \lambda_{i} \] 其中 \(x_{i}^{T}x_{j}\) 正是一个内积操作,通过高维映射后,应该计算的是 \(\phi\left(x_{i}\right)^{T} \phi\left(x_{j}\right)\)。但是如果我们精心设计出一个合理的映射过程 \(\phi\),使得新空间的内积计算复杂度等同于原空间内积计算复杂度,就太好了。
Kernel Trick
Kernel Trick 其实不仅仅针对 SVM。只要目标函数里有这么一个内积的项,就可以使用。它有很多种形式——
- Linear Kernel: \(K(x,y) = x^T y\)
- 数据样本非常多时,用 Linear Kernel 效果会很好。
- Polynomial Kernel: \(K(x,y) = (1+x^Ty)^d\)
- Gaussian Kernel: \(K(x,y)=\exp(\frac{-\|x-y\|^2}{2\sigma^2})\)
那么我们怎么设计映射关系 \(\phi\) (比如上面的 \(\left(x_{1}, x_{2}\right) \rightarrow\left(x_{1}^{2},x_{2}^{2}, \sqrt{2} x_{1} x_{2}\right)\))来满足 Kernel Trick 呢?请看 Mercer's Theorem。
