1 Introduction

Book: Programming in Haskell 2ndEdition

1.1 Functional Programming

What is functional programming?

Functional programming is style of programming in which the basic method of computation is the application of functions to arguments;
A functional language is one that supports and encourages the functional style.

1.2 Features of Haskell

Concise programs (ch2 & ch4)
Powerful type system (ch3 & ch8)
List comprehensions (ch5)
Recursive functions (ch6)
Higher-order functions (ch7)
Effectful functions (ch10 & ch12)
Generic functions (ch12 & ch14)
Lazy evaluation (ch15)
Equational reasoning (ch16 & ch17)

1.3 A Taste of Haskell

sum [] = 0
sum (n:ns) = n + sum ns

type:
Num a => [a] -> a

  sum [1,2,3]
= 1 + sum [2,3]
= 1 + (2 + sum [3])
= 1 + (2 + (3 + sum []))
= 1 + (2 + (3 + 0))
= 6

2 First Steps

2.1 Installation

1
2
3

$ ghci
GHCi, version 8.2.2: http://www.haskell.org/ghc/  :? for help
Prelude>

2.2 Standard Prelude

> head [1,2,3,4,5]
1

> tail [1,2,3,4,5]
[2,3,4,5]

> [1,2,3,4,5] !! 2
3

> take 3 [1,2,3,4,5]
[1,2,3]

> drop 3 [1,2,3,4,5]
[4,5]

> length [1,2,3,4,5]
5

> sum [1,2,3,4,5]
15

> product [1,2,3,4,5]
120

> [1,2,3] ++ [4,5]
[1,2,3,4,5]

> reverse [1,2,3,4,5]
[5,4,3,2,1]

> 1:[2,3,4,5]
[1,2,3,4,5]

More most commonly used definitions see appendix B.

2.3 Function Application

In mathematics: f(a, b) + c d means apply the function f to a and b, and add the result to the product of c and d.

In Haskell, function application is denoted using space. Multiplication is denoted using *.

1	f a b + c * d

Priority: function application is the highest. f a + b means (f a) + b rather than f (a + b).

Mathematics	Haskell
f(x)	f x
f(x, y)	f x y
f(g(x))	f (g x)
f(x, g(y))	f x (g y)
f(x)g(y)	f x * g y

Note that in the 2rd and 4th cases. Without parentheses, f g x and f x g y means apply the function f to g and x ( x, g and y).

2.4 Haskell Scripts

-- test.hs
double x = x + x

quadruple x = double (double x)

❯ ghci test.hs
GHCi, version 8.2.2: http://www.haskell.org/ghc/  :? for help
[1 of 1] Compiling Main             ( test.hs, interpreted )
Ok, one module loaded.
*Main> quadruple 10
40
*Main> take (double 2) [1,2,3,4,5,6]
[1,2,3,4]

-- test.hs
double x = x + x

quadruple x = double (double x)

factorial n = product [1..n]

average ns = sum ns `div` length ns -- x `f` y is just syntactic sugar for f x y.

*Main> factorial 10
3628800
*Main> average [1,2,3,4,5]
3

Useful GHCi Commands

Command Meaning

:load name load script name

:relaod reload current script

:set editor name set editor to name

:edit name edit script name

:edit edit current script

:type expr show type of expr

:? show all commands

:quit quit GHCi

Command	Meaning
:load name	load script name
:relaod	reload current script
:set editor name	set editor to name
:edit name	edit script name
:edit	edit current script
:type expr	show type of expr
:?	show all commands
:quit	quit GHCi

2.5 Naming Requirements

Function and argument names must begin with a lower-case letter.
- myFun
- fun1
- arg_2
- x'
By convention, list arguments usually have an s suffix on their name.
- xs (a list of arbitrary values)
- ns (a list of numbers)
- nss (a list of lists of numbers)
- css (a list of lists of characters)

2.6 The Layout Rule

-- In a sequence of definitions, each definition must begin in precisely the same column:
a = 10
b = 20
c = 30

{-
The layout rule avoids the need for explicit syntax to indicate the grouping of definitions.
-}
-- Implicit grouping:
a = b + c
    where
      b = 1
      c = 2
d = a * 2

-- Explicit grouping
a = b + c
    where
      {b = 1;
       c = 2}
d = a * 2

1 2	-- Combined into a single line: a = b + c where {b = 1; c =2}; d = a * 2

3 Types and Classes

3.1 Types

A type is a name for a collection of related values. Examples:
- the type Bool contains the two logical values False and True.
- the type Bool -> Bool contains all functions that map arguments from Bool to results from Bool (like the logical negation function not)
v :: T means that v is a value in the type T, and say that v has a type T. Examples:
- False :: Bool
- True :: Bool
- not :: Bool -> Bool
More generally, e :: T means that evaluation of the expression e will produce a value of type T. Example:
- not False :: Bool
- not Ture :: Bool
- not (not False) :: Bool

Every well formed expression has a type, which can be automatically calculated at compile time using a process called type inference.

In GHCi, the :type command calculates the type of an expression, without evaluating it:
1
2
3
4
5
6
> :type not
not :: Bool -> Bool
> :type False
False :: Bool
> :type not False
not False :: Bool

3.2 Basic Types

Type	Meaning
`Bool`	logical values
`Char`	single characters
`String`	strings of characters
`Int`	fixed-precision integers (`2147483647` ~ `-2147483647` for 32-bit machine)
`Integer`	arbitrary-precision integers (no bound but with lower efficiency)
`Float`	single-precision floating-point numbers
`Double`	double-precision floating-point numbers

3.3 List Types

A list is a sequence of elements of the same type. [t] is the type of lists with elements of type t. Examples:
- [False, False, Ture] :: [Bool]
- ['a', 'b', 'c', 'd'] :: [Char]
- [['a'], ['b', 'c']] :: [[Char]]

3.4 Tuple Types

A tuple is a sequence of values of different types. (t1,t2,...,tn) is the type of n-tuples whose ith components have type ti for any i in 1…n. Examples:
- (False,True) :: (Bool,Bool)
- (False,'a',True) :: (Bool,Char,Bool)
- ('a',(False,'b')) :: (Char,(Bool,Char))
- (True,['a','b']) :: (Bool,[Char])

3.5 Function Types

A function is a mapping from values of one type to values of another type. t1 → t2 is the type of functions that map values of type t1 to values to type t2. Examples:
- not :: Bool → Bool
- even :: Int → Bool
- add :: (Int,Int) → Int
  - add (x,y) = x+y
- zeroto :: Int → [Int]
  - zeroto n = [0..n]

3.6 Curried Fucntions

Functions with multiple arguments are also possible by returning functions as results. Functions that take their arguments one at a time are called curried functions. Examples:
- add' :: Int → (Int → Int)
  - add' x y = x + y
  add' takes an integer x and returns a function add' x. In turn, this function takes
  
  an integer y and returns the result x+y.
  
  Comparison:
  - add :: (Int, Int) -> Int
- mult :: Int -> (Int -> (Int -> Int))
  - mult x y z = x * y * z

To avoid excess parentheses when working with curried functions, two conventions are adopted:

The funciton arrow -> in types is assumed to associate to the right.

Int -> Int -> Int -> Int means Int -> (Int -> (Int -> Int))

Consequently, function application, which is denoted silently using spacing, is assumed to associated to the left.

mult x y z means ((mult x) y) z

Unless tupling is explicitly required, all functions in Haskell with multiple arguments are normally defined as curried functions.

3.7 Polymorphic Types

A function is called polymorphic (“of many forms”) if its type contains one or more type variables. Examples:
- length :: [a] → Int
- fst :: (a,b) → a
- head :: [a] → a
- take :: Int → [a] → [a]
- zip :: [a] → [b] → [(a,b)]
- id::a → a

3.8 Overloaded Types

A polymorphic function is called overloaded if its type contains one or more class constraints. Examples:
- (+) :: Num a ⇒ a -> a -> a
For any numeric type a, (+) takes two values of type a and returns a value of type a.
- (==) :: Eq a ⇒ a → a → Bool
- (<) :: Ord a ⇒ a → a → Bool
- negate :: Num a => a -> a
- abs :: Num a => a -> a
- 3 :: Num a => a

3.9 Classes

A class is a collection of types that support certain overloaded operations called methods.

3.10 Basic Classes

Class	Meaning
`Eq`	equality types (`/=`, `==`)
`Ord`	ordered types (`<`, `>`, `<=`, `>=`)
`Show`	showable types
`Read`	readable types
`Num`	numeric types
Integral	integral types
`Fractional`	fractional types

4 Defining Functions

4.1 New from Old

The most straightforward way to define new functions is simply by combining one or more existing functions.

Decide if an integer is even:
- even :: Integral a => a -> Bool
- even n = n `mod` 2 == 0
Split a list at the nth element:
- splitAt :: Int -> [a] -> ([a], [a])
- splitAt n xs = (take n xs, drop n xs)
Reciprocation:
- recip :: Fractional a => a -> a
- recip n = 1/n

4.2 Conditional Expressions

As in most programming languages, functions can be defined using conditional expressions.

The absolute value of an integer:
- abs :: Int -> Int
- abs n = if n >= 0 then n else -n

The sign of an integer:

signum :: Int -> Int

```haskell signum n = if n < 0 then -1 else if n == 0 then 0 else 1


> In Haskell, conditional expressions must <u>always</u> have an <u>else</u> branch, which avoids any possible ambiguity problems with nested conditionals. 

## 4.3 Guarded Equations

As an alternative to conditionals, functions can also be defined using <u>guarded equations</u>.

- The absolute value of an integer:

  - ```haskell
    abs n | n >= 0    = n
          | otherwise = -n

The sign of an integer:

```haskell signum n | n < 0 = n | n == 0 = 0 | otherwise = 1


- The BMI calculator:

  - ```haskell
    bmiTell :: (RealFloat a) => a -> a -> String
    bmiTell weight height
        | bmi <= skinny = "You're underweight, you emo, you!"
        | bmi <= normal = "You're supposedly normal. Pffft, I bet you're ugly!"
        | bmi <= fat = "You're fat! Lose some weight, fatty!"
        | otherwise = "You're a whale, congratulations!"
            where bmi = weight / height ^ 2
                  skinny = 18.5
                  normal = 25.0
                  fat = 30.0
                  
    -- can also define functions in `where` statements
    calcBmis :: (RealFloat a) => [(a, a)] -> [a]
    calcBmis xs = [bmi w h | (w, h) <- xs]
         where bmi weight height = weight / height ^ 2

The names teller:

```haskell initials :: String -> String -> String initials firstname lastname = [f] ++ ". " ++ [l] ++ "." where (f:) = firstname (l:) = lastname


  - 

> The catch all condition <u>otherwise</u> is defined in the prelude by `otherwise = True`. 

## 4.4 Pattern Matching

Many functions have a particularly clear definition using <u>pattern matching</u> on their arguments.

- The negation of a logical value:

  - ```haskell
    not :: Bool -> Bool
    not False = True
    not True  = False

The conjunction of two logical values:

```haskell (&&) :: Bool → Bool → Bool True && True = True True && False = False False && True = False False && False = False
1
2
3
4
5

- ```haskell
-- can be defined more compactly by
True && True = True
_ && _ = False

```haskell -- can be defined more efficiently by Ture && b = b Flase && _ = False


    > The underscore symbol _ is a wildcard pattern that matches any argument value. 

> Patterns are matched in order. For example, the following definition always returns False:
>
> ```haskell
> _    && _    = False
> True && True = True

> > Patterns may not repeat variables. For example, the following definition gives an error: > >

1 2	b && b = b _ && _ = False

4.5 Tuple Patterns

A tuple of patterns is itself a pattern, which matches any tuple of the same arity whose components all match the corresponding patterns in order.

Select the first and second components of a pair:
- ```haskell fst :: (a, b) -> a fst (x, _) = x
1
2
3
4

- ```haskell
snd :: (a, b) -> a
snd (_, y) = y

4.6 List Patterns

A list of patterns is itself a pattern, which matches any list of the same length whose elements all match the corresponding patterns in order.

Decide if a list contains precisely three characters beginning with the letter "a":

```haskell test :: [Char] -> Bool test ['a', , ] = True test _ = False

-- more generally: test :: [Char] -> Bool test ['a':_] = True test _ = False


- Internally, every non-empty list is constructed by repeated use of an operator (:) called “cons” that adds an element to the start of a list:

  - `[1,2,3,4]` means `1:(2:(3:(4:[])))`

- Functions on lists can be defined using x:xs patterns:

  - ```haskell
    head :: [a] -> a
    head (x:_) = x
    tail :: [a] -> [a]
    tail (_:xs) = xs

```haskell capital :: String -> String capital "" = "Empty string, whoops!" capital all@(x:xs) = "The first letter of " ++ all ++ " is " ++ [x]
1
2
3
4

```bash
> capital "Dracula"
"The first letter of Dracula is D"

x:xs patterns only match non-empty lists

x:xs patterns must be parenthesised, because application has priority over (:). For example, the following definition gives an error:
1
head x:_ = x

4.7 Lambda Expressions

Functions can be constructed without naming the functions by using lambda expressions.

The nameless function that takes a number x and returns the result x + x:

λx → x + x

```haskell -- typed version -> x + x


- Lambda expressions can be used to give a formal meaning to functions defined using currying:

  - `add x y = x + y` means `add = λx → (λy → x + y)`

- Lambda expressions are also useful when defining functions that return functions as results:

  - ```haskell
    const :: a -> b -> a
    const x _ = x
    
    -- more natrually defined by
    
    const :: a -> (b -> a)
    const x = \_ -> x

Lambda expressions can be used to avoid naming functions that are only referenced once:

```haskell odds n = map f [0..n-1] where f x = x*2 + 1

-- can be simplified to

odds n = map (-> x*2 + 1) [0..n-1]


## 4.8 Operator Sections

An operator written <u>between</u> its two arguments can be converted into a <u>curried function</u> written <u>before</u> its two arguments by using parentheses.

- Addition:

  - ```bash
    > 1+2
    3
    > (+) 1 2
    3

This convention also allows one of the arguments of the operator to be included in the parentheses:

```bash > (1+) 2 3 > (+2) 1 3


> In general, if ⊕ is an <u>operator</u> then functions of the form (⊕), (x⊕) and (⊕y) are called <u>sections</u>.

- Useful functions can sometimes be constructed in a simple way using sections:

  - ```haskell
    (1+) -- successor function
    (1/) -- reciprocation function
    (*2) -- doubling function
    (/2) -- halving function

5 List Comprehensions

5.1 Set Comprehensions

In mathematics, the comprehension notation can be used to construct new sets from old sets:

{x² | x ∈ {1..5}}

The set {1,4,9,16,25} of all numbers x² such that x is an element of the set {1...5}.

5.2 List Comprehensions

In Haskell, a similiar comprehension notation can be used to construct new lists from existing lists:

> [x^2 | x <- [1..5]]
[1,4,9,16,25]
# Comprehensions can have multiple generators, separated by commas:
> [(x,y) | x <- [1,2,3], y <- [4,5]]
[(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)]
# Changing the order of the generators changes the order of the elements in the final list:
> [(x,y) | y <- [4,5], x <- [1,2,3]]
[(1,4),(2,4),(3,4),(1,5),(2,5),(3,5)]
# Multiple generators are like nested loops, with later generators as more deeply nested loops whose variables change value more frequently.

| is read as such that
<- is read as is drawn from
x <- [1..5] is called a generator

> let nouns = ["hobo","frog","pope"]

> let adjectives = ["lazy","grouchy","scheming"]

> [adjective ++ " " ++ noun | adjective <- adjectives, noun <- nouns]

["lazy hobo","lazy frog","lazy pope","grouchy hobo","grouchy frog", "grouchy pope","scheming hobo",

"scheming frog","scheming pope"]

5.3 Dependant Generators

Later generators can depend on the variables that are introduced by earlier generators:

1 2	> [(x,y) \| x <- [1..3], y <- [x..3]] [(1,1),(1,2),(1,3),(2,2),(2,3),(3,3)]

Using a dependant generator we can define the library function that concatenates a list of lists:

1 2	concat :: [[a]] -> [a] concat xss = [x \| xs <- xss,x <- xs]

1 2	> concat [[1,2,3],[4,5],[6]] [1,2,3,4,5,6]

5.4 Wildcard Generators

The wildcard pattern _ is sometimes useful in generators to discard certain elements from a list:

1 2	firsts :: [(a,b)] -> [a] firsts ps = [x \| (x,_) <- ps]

Similarly, the library function that calculates the length of a list:

1 2	length :: [a] -> Int length xs = sum [1 \| _ <- xs]

5.5 Guards

List comprehensions can use guards to restrict the values produced by earlier generators:

1 2	> [x \| x <- [1..10], even x] [2,4,6,8,10]

Using a guard we can define a function that maps a positive integer to its list of factors:

1
2
3

factors :: Int -> [Int]
factors n =
    [x | x <- [1..n], n `mod` x == 0]

1 2	> factors 15 [1,3,5,15]

A positive integer is prime if its only factors are 1 and itself. Hence, using factors we can define a function that decides if a number is prime:

1 2	prime :: Int -> Bool prime n = factors n == [1,n]

Using a guard we can now define a function that returns the list of all primes up to a given limit:

1 2	primes :: Int -> [Int] primes n = [x \| x <- [2..n], prime x]

Suppose we represent a lookup table by a list of pairs of keys and values. Then for any type of keys that supports equality, a function find that returns the list of all values that are associated with a given key in a table can be defined as:

1 2	find :: Eq a => a -> [(a, b)] -> [b] find k t = [v \| (k', v) <- t, k == k']

1 2	> find 'b' [('a',1),('b',2),('c',3),('b',4)] [2,4]

5.6 The `zip` Function

A useful library function is zip, which maps two lists to a list of pairs of their corresponding elements:

1	zip :: [a] -> [b] -> [(a,b)]

> zip [’a’,’b’,’c’] [1,2,3,4]
[(’a’,1),(’b’,2),(’c’,3)]
> zip [1..] ["apple", "orange", "cherry", "mango"]
[(1,"apple"),(2,"orange"),(3,"cherry"),(4,"mango")]

Using zip we can define a function returns the list of all pairs of adjacent elements from a list:

1 2	pairs :: [a] -> [(a,a)] pairs xs = zip xs (tail xs)

1 2	> pairs [1,2,3,4] [(1,2),(2,3),(3,4)]

Using pairs we can define a function that decides if the elements in a list are sorted:

1 2	sorted :: Ord a => [a] -> Bool sorted xs = and [x <= y \| (x,y) <- pairs xs]

> sorted [1,2,3,4]
True
> sorted [1,3,2,4]
False

Using zip we can define a function that returns the list of all positions of a value in a list:

1 2	positions::Eqa => a -> [a] -> [Int] positions x xs = [i \| (x',i) <- zip xs [0..], x == x']

1 2	> positions 0 [1,0,0,1,0,1,1,0] [1,2,4,7]

5.7 String Comprehensions

A string is a sequence of characters enclosed in double quotes. Internally, however, strings are represented as lists of characters:

"abc" :: String means ['a', 'b', 'c'] :: [Char]

Because strings are just special kinds of lists, any polymorphic function that operates on lists can also be applied to strings:

> length "abcde"
5
> take 3 "abcde"
"abc"
> zip "abc" [1,2,3,4]
[('a',1),('b',2),('c',3)]

Similarly, list comprehensions can also be used to define functions on strings, such counting how many times a character occurs in a string:

1 2	count :: Char -> String -> Int count xxs = length [x' \|x' <- xs , x == x']

1 2	> count 's' "Mississippi" 4

5.8 Some Notes

[1,2,3] is the syntax sugar for 1:2:3:[]
```bash # Compare the first elements in two lists, if equals, compare next one, so on and so forth > [3,2,1] > [2,1,0] True > [3,2,1] > [2,10,100] True > [3,4,2] > [3,4] True > [3,4,2] > [2,4] True > [3,4,2] == [3,4,2] True
1
2
3
4
5
6
7
8

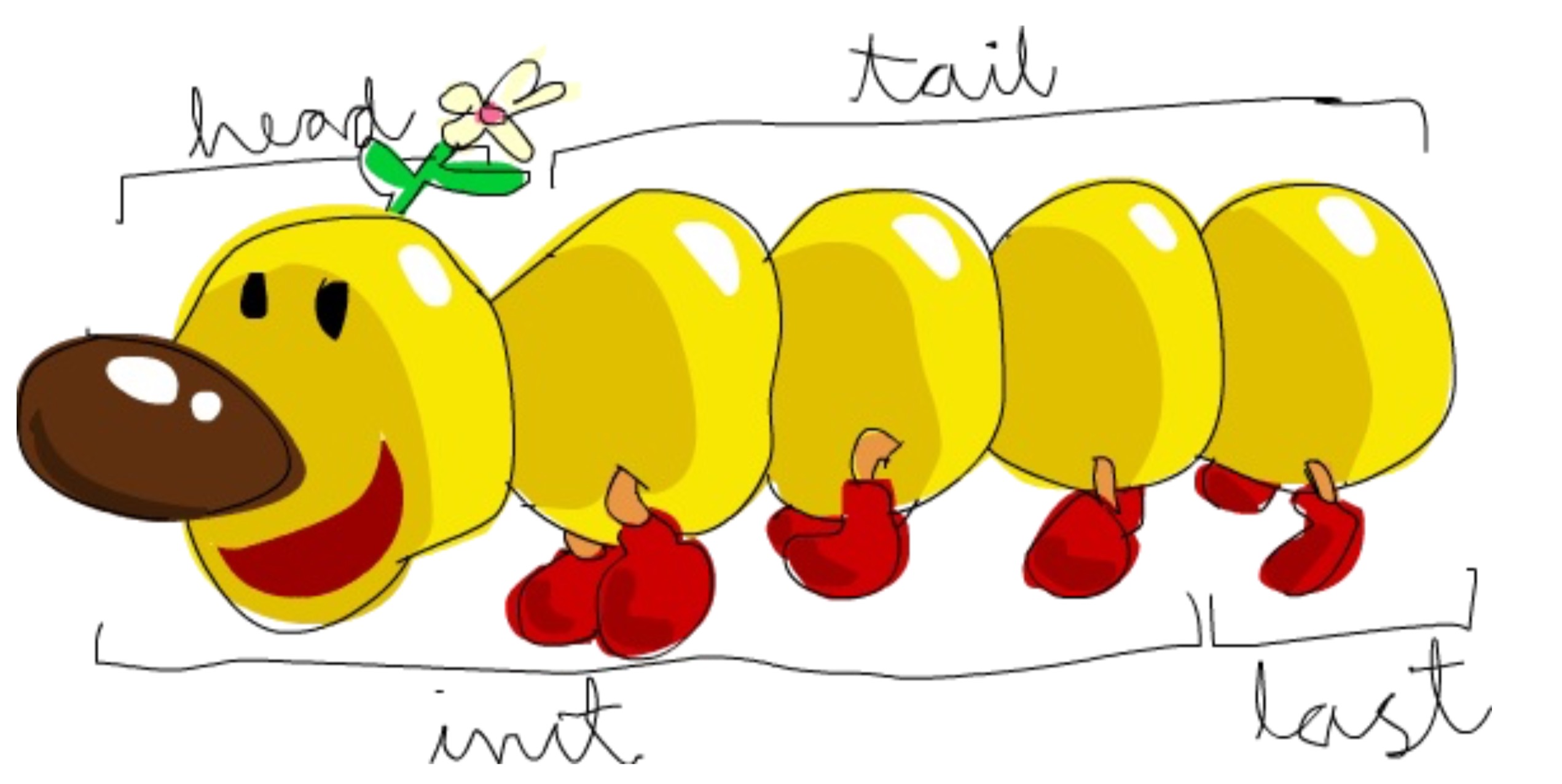
- ![](https://i.loli.net/2018/05/21/5b020f6672a28.png)

- Avoid using `xs == []` but using `null a_list` to check if a list is empty

- ```bash
> 4 `elem` [3,4,5,6]
True

```bash > [1,20] [1,20] > [2,4..20] [2,4,6,8,10,12,14,16,18,20] > [20,19..1] [20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1] > take 24 [13,26..] [13,26,39,52,65,78,91,104,117,130,143,156,169,182,195,208,221,234,247,260,273,286,299,312] # No floating numbers when using range > [0.1,0.3..1] [0.1,0.3,0.5,0.7,0.8999999999999999,1.0999999999999999] > take 10 (cycle [1,2,3]) [1,2,3,1,2,3,1,2,3,1] > take 10 (repeat 5) [5,5,5,5,5,5,5,5,5,5] > replicate 10 3 [3,3,3,3,3,3,3,3,3,3]


- 

# 6 Recursive Functions

## 6.1 Basic Concepts

In Haskell, functions can also be defined in terms of themselves. Such functions are called <u>recursive</u>:

```haskell
fac 0 = 1
fac n = n * fac (n-1)

The recursive definition diverges on integers < 0 because the base case is never reached:
1
2
> fac (-1)
*** Exception: stack overflow

6.2 Recursion on Lists

Recursion is not restricted to numbers, but can also be used to define functions on lists:

1
2
3

product :: Num a => [a] -> a
product [] = 1
product (n:ns) = n * product ns

1 2	> product [2,3,4] 24

Using the same pattern of recursion as in product we can define the length function on lists:

1
2
3

length :: [a] -> Int
length [] = 0
length (_:xs) = 1 + length xs

Using a similar pattern of recursion we can define the reverse function on lists:

1
2
3

reverse :: [a] -> [a]
reverse [] = []
reverse (x:xs) = reverse xs ++ [x]

In turn, the append operator ++ can itself be defined using recursion on its first argument:

1
2
3

(++) :: [a] -> [a] -> [a]
[] ++ ys = ys
(x:xs) ++ ys = x : (xs ++ ys)

More examples:

maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs)
    | x > maxTail = x
    | otherwise = maxTail
    where maxTail = maximum' xs
-- or:
maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs) = max x (maximum' xs)

6.3 Multiple Arguments

Functions with more than one argument can also be defined using recursion:

Zipping the elements of two lists:

zip :: [a] -> [b] -> [(a,b)]
zip [] _ = []
zip _ [] = []
zip (x:xs) (y:ys) = (x,y) : zip xs ys

Remove the first n elements from a list:

drop :: Int -> [a] -> [a]
drop 0 xs = xs
drop _ [] = []
drop n (_:xs) = drop (n-1) xs

Appending two lists:

1
2
3

(++) :: [a] -> [a] -> [a]
[] ++ ys = ys
(x:xs) ++ ys = x : (xs ++ ys)

6.4 Multiple Recursion

Functions can also be defined using multiple recursions:

fib :: Int -> Int
fib 0 = 0
fib 1 = 1
fib n = fib (n - 2) + fib (n - 1)

The quicksort algorithm for sorting a list of values can be specified by the following two rules:

The empty list is already sorted;
Non-empty lists can be sorted by sorting the tail values ≤ the head, sorting the tail values > the head, and then appending the resulting lists on either side of the head value.

Using recursion, this specification can be translated directly into an implementation:

qsort :: Ord a => [a] -> [a]
qsort [] = []
qsort (x:xs) = qsort smaller ++ [x] ++ qsort larger
               where
                   smaller = [a | a <- xs,a <= x]
                   larger  = [b | b <- xs,b > x]

6.5 Mutual Recursion

Functions can also be defined using mutual recursion, in which two or more functions are all defined recursively in terms of each other:

even :: Int -> Bool
even 0 = True
even n = odd (n - 1)

odd :: Int -> Bool
odd 0 = False
odd n = even (n - 1)

Similarly, functions that select the elements from a list at all even and odd positions (counting from zero) can be defined as:

evens :: [a] -> [a]
evens [] = []
evens (x:xs) = x : odds xs

odds :: [a] -> [a]
odds [] = []
odds (_:xs) = evens xs

7 Higher-Order Functions

7.1 Basic Concepts

A function is called higher-order if it takes a function as an argument or returns a function as a result:

twice :: (a -> a) -> a -> a
twice f x = f (f x)

flip :: (a -> b -> c) -> (b -> a -> c)
flip f = g
    where g x y = f y x
-- or
flip :: (a -> b -> c) -> b -> a -> c
flip f y x = f x y
-- or
flip :: (a -> b -> c) -> b -> a -> c
flip f = \x y -> f y x

> twice (*2) 3
12
> twice reverse [1,2,3]
[1,2,3]

Why Are They Useful?

Common programming idioms can be encoded as functions within the language itself.

Domain specific languages can be defined as collections of higher-order functions.

Algebraic properties of higher-order functions can be used to reason about programs.

7.2 Processing Lists

7.2.1 The `map` Function

The higher-order library function called map applies a function to every element of a list:

map :: (a -> b) -> [a] -> [b]

-- The map function can be defined in a particularly simple manner using a list comprehension:
map f xs = [f x | x <- xs]

-- Alternatively, for the purposes of proofs, the map function can also be defined using recursion:
map f [] = []
map f (x:xs) = f x : map f xs

1 2	> map (+1) [1,3,5,7] [2,4,6,8]

7.2.2 The `filter` Function

The higher-order library function filter selects every element from a list that satisfies a predicate:

filter :: (a -> Bool) -> [a] -> [a]

-- Filter can be defined using a list comprehension:
filter p xs = [x | x <- xs, px]
-- Alternatively, it can be defined using recursion:
filter p [] = []
filter p (x:xs)
   | p x       = x : filter p xs
   | otherwise = filter p xs

> filter even [1..10]
[2,4,6,8,10]
> filter (> 5) [1..10]
[6,7,8,9,10]
> filter (/= ' ') "abc def ghi"
"abcdefghi"

7.2.3 The `foldr` Function

回到当初我们学习递归的情景。我们会发现处理 List 的许多函数都有固定的模式，通常我们会将边界条件设置为空 List，再引入 (x:xs) 模式，对单个元素和余下的 List 做些事情。这一模式是如此常见，因此 Haskell 引入了一组函数来使之简化，也就是 fold 。它们与 map 有点像，只是它们回传的是单个值。

A number of functions on lists can be defined using the following simple pattern of recursion:

1 2	f [] = v f (x:xs) = x ⊕ f xs

f maps the empty list to some value v, and any non-empty list to some function ⊕ applied to its head and f of its tail. Examples:
1
2
3
4
5
6
7
8
sum [] = 0
sum (x:xs) = x + sum xs

product []     = 1
product (x:xs) = x * product xs

and []     = True
and (x:xs) = x && and xs

The higher-order library function foldr (fold right) encapsulates this simple pattern of recursion, with the function ⊕ and the value v as arguments:

sum = foldr (+) 0
product = foldr (*) 1
or = foldr (||) False
and = foldr (&&) True

Foldr itself can be defined using recursion:

1
2
3

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f v [] = v
foldr f v (x:xs) = f x (foldr f v xs)

However, it is best to think of foldr non-recursively, as simultaneously replacing each (:) in a list by a given function, and [] by a given value. Example:

-- replace each (:) by (*) and [] by 1
  product [1,2,3]
= foldr (*) 1 [1,2,3]
= foldr (*) 1 (1:(2:(3:[])))
= 1*(2*(3*1))
= 6

Other Foldr Examples

Even though foldr encapsulates a simple pattern of recursion, it can be used to define many more functions than might first be expected. Recall the length function:
1
2
3
4
5
-- Replace each (:) by λ_ n → 1+n and [] by 0.
  length [1,2,3]
= length (1:(2:(3:[])))
= 1+(1+(1+0))
= 3
Hence, we have:
1
length = foldr (\_ n -> 1 + n) 0
...
1
reverse = foldr (\x xs -> xs ++ [x]) []
Finally, we note that the append function (++) has a particularly compact definition using foldr:
1
(++ ys) = foldr (:) ys

Why Is Foldr Useful?

Some recursive functions on lists, such as sum, are simpler to define using foldr.

Properties of functions defined using foldr can be proved using algebraic properties of foldr, such as fusion and the banana split rule.

Advanced program optimisations can be simpler if foldr is used in place of explicit recursion.

7.2.4 The `foldl` Function

7.3 The Composition Operator

The library function . returns the composition of two functions as a single function:

1 2	(.) :: (b -> c) -> (a -> b) -> (a -> c) f . g = \x -> f (g x)

Example:

odd = not . even

twice f = f . f

sumsqreven = sum . map (^2) . filter even
-- sumsqreven = sum (map (^2) (filter even))

fn = ceiling . negate . tan . cos . max 50
-- fn x = ceiling (negate (tan (cos (max 50 x))))

1	f . (g . h) == (f . g) . h

7.4 Some Other Library Functions

7.4.1 The `all` Function

The library function all decides if every element of a list satisfies a given predicate:

1 2	all :: (a -> Bool) -> [a] -> Bool all p xs = and [p x \| x <- xs]

1 2	> all even [2,4,6,8,10] True

7.4.2 The `any` Function

Dually, the library function any decides if at least one element of a list satisfies a predicate:

1 2	any :: (a -> Bool) -> [a] -> Bool any p xs = or [px \| x <- xs]

1 2	> any (== ' ') "abc def" True

7.4.3 The `takeWhile` Function

The library function takeWhile selects elements from a list while a predicate holds of all the elements:

takeWhile :: (a -> Bool) -> [a] -> [a]
takeWhile p [] = []
takeWhile p (x:xs)
   | p x       = x : takeWhile p xs
   | otherwise = []

> takeWhile (/= ' ') "abc def"
"abc"
> sum (takeWhile (<10000) (filter odd (map (^2) [1..])))
166650
# or
> sum (takeWhile (<10000) [m | m <- [n^2 | n <- [1..]], odd m])
166650

7.4.4 The `dropWhile` Function

Dually, the function dropWhile removes elements while a predicate holds of all the elements:

dropWhile :: (a -> Bool) -> [a] -> [a]
dropWhile p [] = []
dropWhile p (x:xs)
   | p x       = dropWhile p xs
   | otherwise = x:xs

1 2	> dropWhile (== ' ') " abc" "abc"

8 Declaring Types and Classes

8.1 Type Declarations

A new name for an existing type can be defined using a type declaration:

1	type String = [Char] -- String is a synonym for the type [Char].

Type declarations can be used to make other types easier to read. For example, given:

1 2	type Pos = (Int,Int) type Trans = Pos -> Pos

we can define:

origin :: Pos
origin = (0,0)

left :: Trans
left (x,y) = (x-1,y)

However, type declarations cannot be recursive.
1
type Tree = (Int, [Tree]) -- Wrong!

Like function definitions, type declarations can also have parameters. For example, given:

1	type Pair a = (a,a)

we can define:

mult :: Pair Int -> Int
mult (m,n) = m*n

copy :: a -> Pair a
copy x = (x,x)

Example: a phone book type:

type PhoneNumber = String
type Name = String
type PhoneBook = [(Name,PhoneNumber)]

inPhoneBook :: Name -> PhoneNumber -> PhoneBook -> Bool
inPhoneBook name pnumber pbook = (name,pnumber) `elem` pbook

8.2 Data Declarations

A completely new type can be defined by specifying its values using a data declaration:

1	data Bool = False \| True -- Bool is a new type, with two new values False and True.

The two values False and True are called the value constructors for the type Bool.

Type and constructor names must always begin with an upper-case letter.

Data declarations are similar to context free grammars. The former specifies the values of a type, the latter the sentences of a language.

Values of new types can be used in the same ways as those of built in types. For example, given:

1	data Answer = Yes \| No \| Unknown

we can define:

answers :: [Answer]
answers = [Yes,No,Unknown]

flip :: Answer -> Answer
flip Yes = No
flip No = Yes
flip Unknown = Unknown

The constructors in a data declaration can also have parameters. For example, given:

1	data Shape = Circle Float \| Rect Float Float

we can define:

square :: Float -> Shape
square n = Rect n n

area :: Shape -> Float
area (Circle r) = pi * r^2
area (Rect x y) = x * y

Shape has values of the form Circle r where r is a float, and Rect x y where x and y are floats.
Circle and Rect can be viewed as functions that construct values of type Shape:
1
2
Circle :: Float -> Shape
Rect :: Float -> Float -> Shape

Data declarations themselves can also have parameters. For example, given:

data Maybe a = Nothing | Just a

-- Nothing :: Maybe a
-- Just :: a -> Maybe a

we can define:

safediv :: Int -> Int -> Maybe Int
safediv _ 0 = Nothing
safediv m n = Just (m `div` n)

safehead :: [a] -> Maybe a
safehead [] = Nothing
safehead xs = Just (head xs)

8.3 Newtype Declarations

If a new type has a single constructor witha single argument, then it can also be declared using the newtype mechanism.

For example, a type of natural numbers:

newtype Nat = N Int -- the single constructor N takes a single argument of type Int

-- alternative versions:
type Nat = Int
data Nat = N Int

-- differences:
-- 1. newtype but not type means different types rather than synonyms
-- 2. newtype but not data means an efficiency benefit

8.4 Recursive Types

Types can be recursive through data or newtype declarations:

1 2	data Nat = Zero \| Succ Nat -- Nat is a new type, with constructors Zero :: Nat and Succ :: Nat → Nat.

A value of type Nat is either Zero, or of the form Succ n where n :: Nat. That is, Nat contains the following infinite sequence of values:
1
2
3
4
Zero
Succ Zero
Succ (Succ Zero)
...
We can think of values of type Nat as natural numbers, where Zero represents 0, and Succ represents the successor function 1+:
1
2
3
  Succ (Succ (Succ Zero))
= 1+(1+(1+0))
= 3

Using recursion, it is easy to define functions that convert between values of type Nat and Int:

nat2int :: Nat -> Int
nat2int Zero = 0
nat2int (Succ n) = 1 + nat2int n

int2nat :: Int -> Nat
int2nat 0 = Zero
int2nat n = Succ (int2nat (n-1))

Two naturals can be added by converting them to integers, adding, and then converting back:

1 2	add::Nat -> Nat -> Nat add m n = int2nat (nat2int m + nat2int n)

However, using recursion the function add can be defined without the need for conversions:

1 2	add Zero n = n add (Succ m) n = Succ (add m n)

  add (Succ (Succ Zero)) (Succ Zero)
= Succ (add (Succ Zero) (Succ Zero))
= Succ (Succ (add Zero (Succ Zero))
= Succ (Succ (Succ Zero))

8.5 Arithmetic Expressions

Using recursion, a suitable new type to represent such expressions can be declared by:

1
2
3

data Expr = Val Int
          | Add Expr Expr
          | Mul Expr Expr

Example:

1	Add (Val 1) (Mul (Val 2) (Val 3))

Using recursion, it is now easy to define functions that process expressions. For example:

size :: Expr -> Int
size (Val n) = 1
size (Add x y) = size x + size y
size (Mul x y) = size x + size y

eval :: Expr -> Int
eval (Val n) = n
eval (Add x y) = eval x + eval y
eval (Mul x y) = eval x * eval y

The three constructors have types:
1
2
3
Val :: Int -> Expr
Add :: Expr -> Expr -> Expr
Mul :: Expr -> Expr -> Expr
Many functions on expressions can be defined by replacing the constructors by other functions using a suitable fold function. For example:
1
eval = folde id (+) (*)

8.6 Binary Trees

In computing, it is often useful to store data in a two-way branching structure or binary tree.

Using recursion, a suitable new type to represent such binary trees can be declared by:

1	data Tree a = Leaf a \| Node (Tree a) a (Tree a)

1
2
3

t :: Tree Int
t = Node (Node (Leaf 1) 3 (Leaf 4)) 5
         (Node (Leaf 6) 7 (Leaf 9))

We can now define a function that decides if a given value occurs in a binary tree:

occurs :: Ord a => a -> Tree a -> Bool
occurs x (Leaf y) = x == y
occurs x (Node l y r) = x == y
                        || occurs x l
                        || occurs x r

But... in the worst case, when the value does not occur, this function traverses the entire tree.

Now consider the function flatten that returns the list of all the values contained in a tree:

flatten :: Tree a -> [a]
flatten (Leaf x) = [x]
flatten (Node l x r) = flatten l
                       ++ [x]
                       ++ flatten r

A tree is a search tree if it flattens to a list that is ordered. Our example tree is a search tree, as it flattens to the ordered list [1,3,4,5,6,7,9].

Search trees have the important property that when trying to find a value in a tree we can always decide which of the two sub-trees it may occur in:

occurs x (Leaf y)              = x == y
occurs x (Node l y r) | x == y = True
                      | x < y  = occurs x l
                      | x > y  = occurs x r

This new definition is more efficient, because it only traverses one path down the tree.

9 The Countdown Problem

9.1 Basic Concept

Given a sequence of numbers and a target number, attempt to construct an expression whose value is the target, by combining one or more numbers from the sequence using addition, subtraction, multiplication, division and parentheses.

More Rules:

All the numbers, including intermediate results, must be positive naturals (1,2,3,...).

Each of the source numbers can be used at most once when constructing the expression.

Example:
1
2
3
4
5
6
7
numbers: 1 3 7 10 25 50

arithemetic operators: + - * ÷

target value: 765

one possible solution: (25 - 10) * (50 + 1) = 765

9.2 Evaluating Expressions

Operators:

1	data Op = Add \| Sub \| Mul \| Div

Apply an operator:

apply :: Op -> Int -> Int -> Int
apply Add x y = x + y
apply Sub x y = x - y
apply Mul x y = x * y
apply Div x y = x `div` y

Decide if the result of applying an operator to two positive natural numbers is another such:

valid :: Op -> Int -> Int -> Bool
valid Add _ _ = True
valid Sub x y = x > y
valid Mul _ _ = True
valid Div x y = x `mod` y == 0

Expressions:

1	data Expr = Val Int \| App Op Expr Expr

Return the overall value of an expression, provided that it is a positive natural number:

eval :: Expr -> [Int]
eval (Val n) = [n | n > 0]
eval (App o l r) = [apply o x y | x <- eval l
                                , y <- eval r
                                , valid o x y]
-- Either succeeds and returns a singleton list, or fails and returns the empty list.

9.3 Formalising The Problem

Return a list of all possible ways of choosing zero or more elements from a list:

1	choices :: [a] -> [[a]]

For example:

1 2	> choices [1,2] [[],[1],[2],[1,2],[2,1]]

Return a list of all the values in an expression:

1
2
3

values :: Expr -> [Int]
values (Val n) = [n]
values (App _ l r) = values l ++ values r

Decide if an expression is a solution for a given list of source numbers and a target number:

1
2
3

solution :: Expr -> [Int] -> Int -> Bool
solution e ns n = elem (values e) (choices ns)
                  && eval e == [n]

9.4 Brute Force Solution

Return a list of all possible ways of splitting a list into two non-empty parts:

1	split :: [a] -> [([a],[a])]

For example:

1 2	> split [1,2,3,4] [([1],[2,3,4]),([1,2],[3,4]),([1,2,3],[4])]

Return a list of all possible expressions whose values are precisely a given list of numbers:

exprs :: [Int] -> [Expr]
exprs [] = []
exprs [n] = [Val n]
exprs ns = [e | (ls,rs) <- split ns
              , l       <- exprs ls
              , r       <- exprs rs
              , e       <- combine l r]
--  The key function in this lecture.

Combine two expressions using each operator:

1 2	combine :: Expr -> Expr -> [Expr] combine l r = [App o l r \| o <- [Add,Sub,Mul,Div]]

Return a list of all possible expressions that solve an instance of the countdown problem:

solutions :: [Int] -> Int -> [Expr]
solutions ns n = [e | ns' <- choices ns
                    , e   <- exprs ns'
                    , eval e == [n]]

How Fast Is It?

Can We Do Better?

Many of the expressions that are considered will typically be invalid - fail to evaluate.

For our example, only around 5 million of the 33 million possible expressions are valid.

Combining generation with evaluation would allow earlier rejection of invalid expressions.

9.5 Fusing Two Functions

Valid expressions and their values:

1	type Result = (Expr,Int)

We seek to define a function that fuses together the generation and evaluation of expressions:

1
2
3

results :: [Int] -> [Result]
results ns = [(e,n) | e <- exprs ns
                    , n <- eval e]

This behaviour is achieved by defining:

results []  = []
results [n] = [(Val n,n) | n > 0]
results ns  = [res | (ls,rs) <- split ns
                   , lx      <- results ls
                   , ry      <- results rs
                   , res     <- combine' lx ry]

where:

1	combine' :: Result → Result → [Result]

Combining results:

1
2
3

combine' (l,x) (r,y) = [(App o l r, apply o x y)
                         | o <- [Add,Sub,Mul,Div]
                         , valid o x y]

New function that solves countdown problems:

1 2	solutions' :: [Int] → Int → [Expr] solutions' ns n = [e \| ns' <- choices ns , (e,m) <- results ns' , m == n]

How Fast Is It Now?

Can We Do Better?

Many expressions will be essentially the same using simple arithmetic properties, such as:

x*y = y*x

x*1 = x

Exploiting such properties would considerably reduce the search and solution spaces.

9.6 Exploiting Properties

Strengthening the valid predicate to take account of commutativity and identity properties:

valid :: Op -> Int -> Int -> Bool
valid Add x y = x <= y
valid Sub x y = x > y
valid Mul x y = x <= y && x /= 1 && y /= 1
valid Div x y = x `mod` y == 0 && y /= 1

How Fast Is It Now?

10 Interactive Programming

10.1 Basic Concepts

To date, we have seen how Haskell can be used to write batch programs that take all their inputs at the start and give all their outputs at the end.

However, we would also like to use Haskell to write interactive programs that read from the keyboard and write to the screen, as they are running.

10.2 The Problem

Haskell programs are pure mathematical functions:

Haskell programs have no side effects.

However, reading from the keyboard and writing to the screen are side effects:

Interactive programs have side effects.

10.3 The Solution

Interactive programs can be written in Haskell by using types to distinguish pure expressions from impure actions that may involve side effects.

1 2	IO a -- The type of actions that return a value of type a.

For example:

IO Char
-- The type of actions that return a character.

IO ()
-- The type of purely side effecting actions that return no result value.
-- Note: () is the type of tuples with no components.

10.4 Basic Actions

The standard library provides a number of actions, including the following three primitives:

The action getChar reads a character from the keyboard, echoes it to the screen, and returns the character as its result value:
1
getChar :: IO Char
The action putChar c writes the character c to the screen, and returns no result value:
1
putChar :: Char -> IO ()
The action return v simply returns the value v, without performing any interaction:
1
return :: a -> IO a

10.5 Sequencing

A sequence of actions can be combined as a single composite action using the keyword do:

act :: IO (Char,Char)
act = do x <- getChar
         getChar
         y <- getChar
         return (x,y)

10.6 Derived Primitives

Reading a string from the keyboard:

getLine :: IO String
getLine = do x <- getChar
             if x == '\n' then
                return []
             else
                do xs <- getLine
                   return (x:xs)

Writing a string to the screen:

putStr :: String -> IO ()
putStr [] = return ()
putStr (x:xs) = do putChar x
                   putStr xs

Writing a string and moving to a new line:

1
2
3

putStrLn :: String -> IO ()
putStrLn xs = do putStr xs
                 putChar '\n'

10.7 Example

We can now define an action that prompts for a string to be entered and displays its length:

strlen :: IO ()
strlen = do putStr "Enter a string: "
            xs <- getLine
            putStr "The string has "
            putStr (show (length xs))
            putStrLn " characters"

For example:

1
2
3

> strlen
Enter a string: Haskell
The string has 7 characters

Evaluating an action executes its side effects, with the final result value being discarded.

10.8 Hangman

Consider the following version of hangman:

One player secretly types in a word.
The other player tries to deduce the word, by entering a sequence of guesses.
For each guess, the computer indicates which letters in the secret word occur in the guess.
The game ends when the guess is correct.

We adopt a top down approach to implementing hangman in Haskell, starting as follows:

hangman :: IO ()
hangman = do putStrLn "Think of a word: "
             word <- sgetLine
             putStrLn "Try to guess it:"
             play word

The action sgetLine reads a line of text from the keyboard, echoing each character as a dash:

sgetLine :: IO String
sgetLine = do x <- getCh
              if x == '\n' then
                 do putChar x
                    return []
              else
                 do putChar '-'
                    xs <- sgetLine
                    return (x:xs)

The action getCh reads a single character from the keyboard, without echoing it to the screen:

import System.IO

getCh :: IO Char
getCh = do hSetEcho stdin False
           x <- getChar
           hSetEcho stdin True
           return x

The function play is the main loop, which requests and processes guesses until the game ends.

play :: String -> IO ()
play word =
    do putStr "? "
       guess <- getLine
       if guess == word then
          putStrLn "You got it!"
       else
          do putStrLn (match word guess)
             play word

The function match indicates which characters in one string occur in a second string:

1
2
3

match :: String -> String -> String
match xs ys =
    [if elem x ys then x else '-' | x <- xs]

For example:

1 2	> match "haskell" "pascal" "-as--ll"

1 Introduction

1.1 Functional Programming

1.2 Features of Haskell

1.3 A Taste of Haskell

2 First Steps

2.1 Installation

2.2 Standard Prelude

2.3 Function Application

2.4 Haskell Scripts

2.5 Naming Requirements

2.6 The Layout Rule

3 Types and Classes

3.1 Types

3.2 Basic Types

3.3 List Types

3.4 Tuple Types

3.5 Function Types

3.6 Curried Fucntions

3.7 Polymorphic Types

3.8 Overloaded Types

3.9 Classes

3.10 Basic Classes

4 Defining Functions

4.1 New from Old

4.2 Conditional Expressions

4.5 Tuple Patterns

4.6 List Patterns

4.7 Lambda Expressions

5 List Comprehensions

5.1 Set Comprehensions

5.2 List Comprehensions

5.3 Dependant Generators

5.4 Wildcard Generators

5.5 Guards

5.6 The zip Function

5.7 String Comprehensions

5.8 Some Notes

6.2 Recursion on Lists

6.3 Multiple Arguments

6.4 Multiple Recursion

6.5 Mutual Recursion

7 Higher-Order Functions

7.1 Basic Concepts

7.2 Processing Lists

7.2.1 The map Function

7.2.2 The filter Function

7.2.3 The foldr Function

7.2.4 The foldl Function

7.3 The Composition Operator

7.4 Some Other Library Functions

7.4.1 The all Function

7.4.2 The any Function

7.4.3 The takeWhile Function

7.4.4 The dropWhile Function

8 Declaring Types and Classes

8.1 Type Declarations

8.2 Data Declarations

8.3 Newtype Declarations

8.4 Recursive Types

8.5 Arithmetic Expressions

8.6 Binary Trees

9 The Countdown Problem

9.1 Basic Concept

9.2 Evaluating Expressions

9.3 Formalising The Problem

9.4 Brute Force Solution

9.5 Fusing Two Functions

9.6 Exploiting Properties

10 Interactive Programming

10.1 Basic Concepts

10.2 The Problem

10.3 The Solution

10.4 Basic Actions

10.5 Sequencing

10.6 Derived Primitives

10.7 Example

10.8 Hangman

5.6 The `zip` Function

7.2.1 The `map` Function

7.2.2 The `filter` Function

7.2.3 The `foldr` Function

7.2.4 The `foldl` Function

7.4.1 The `all` Function

7.4.2 The `any` Function

7.4.3 The `takeWhile` Function

7.4.4 The `dropWhile` Function